Batch 3 - Class 120 - Stable Marriage Problem
Pre-Class Problem:
Think about one more game that you like, which can be modeled as Markov Chain. Think about what "states" represent, and how you would create a transition diagram. Think about the elements you would take into account to assign probabilities to transition. Finally, on a simplistic version, try to find probabilities of outcomes. What outcomes are important in your game?
Attendance: Muskaan, Khushi, Anshi, Ahana, Manya, Arnav, Damini, Siddhant, Tishyaa, Liza, Diya, Palak
Class Notes:
There are an equal number of eligible men and women in a village, and all of them need to paired off. Each of the men have a preference list of women to whom they would like to get married, and so do the women. We want to pair them off in a "stable" structure, which means that at the end, there should be no pair where wife of one man wants to be with the other one more, and the other man also prefers her to his wife.
Instructor Notes: Illustrate the problem
Question: Is it always possible to arrive at such a stable structure?
- Let kids work on a 4x4 problem. They may realize that solving for a smaller problem is easier - let them try 2x2 or 3x3
- Some kids may find a solution, and claim it is always possible. What if the preferences were different - would it always be possible?
- How do we arrive at the solution?
- What if we started to give some women their first choice? Then we know that at least they wouldn't want to run away. But we also need to make sure that their husbands don't have a more mutually preferred person elsewhere... May be we let the man then take up the one they get the best one from...
- So step one - let each woman propose to her most preferred man. The man takes all the proposals he receives and holds onto the best one, rejects the others
- Day two - rejected women make their next proposal. If a man gets a proposal from a more preferred woman than he already has, he swaps to hold the new one, else he stays.
- Continue till everyone has an acceptance (will we always get to that point?)
- Lets work through a sample exercise
.png)
- Instructor Notes: Younger kids may want to work through a smaller problem. Remove Collins and Elizabeth from above
- Show step by step offers, and circle the offers on both grids. Cross out the rejections.
- Does this seem to work? Can you notice "progress" at each step, which seems to indicate that the algorithm will terminate?
- Can we prove this works?
- Can we prove that no woman can get a better husband than she already has?
- Every man a particular woman prefers over her husband, actually got a chance to reject her in favor of a more preferred woman!
- Actually the women proposing and getting rejected, gives the best arrangement for women, not for men!Actually, for men, this gives them the worst possible wife (amongst all sets of stable marriage solutions)Can we prove this? (Hard one) What about the first woman who got rejected by a possible husband M(preferred)? If she got assigned to M(actual). It means M(preferred) likes another woman who also proposed to him. For her to be with M(preferred) in some arrangement, the other woman would have to be with M(even better). For that to happen she would have previously proposed to M(even better) and got rejected. So this can not be the first rejection... Hence, proved by contradiction!
- Is this unique? What would happen if the men were proposing and women were rejecting? Let kids try it out.
- (Advanced - don't do in class) Is it possible to lie about one's preference and get a better result? As it happens, if women are proposing, a woman can't get a better result by lying. However, the man can.
Dorm Room Problem
What if there were 4 people and we wanted to pair them into roommates. Can you always find a stable solution to that?
- If yes, prove
- If not, find a counter-example
.png)
- What is the key difference between this and the previous problem?
- Remember, subtle differences in the problem can give very different results.
School Distance Problem
Suppose we wanted to match certain kids to certain schools, each school having fixed capacity, so that each kid gets the nearest possible school to them, and each school gets the nearest possible set of students?
- Is there a stable solution?
- Is it unique?
- In this case, the solution is unique - why? what has changed?
- The criteria for both students and schools is the same!
Homework
(Dudeney 259) A man was in love with a woman named HANNAH. He proposed. She wrote down her name as under.
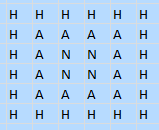
She challenged the suitor to spell her name in as many ways as possible on the above grid, starting from any H and passing from one letter to another adjacent letter, in any direction. How many such ways exist?
- Answer: There are 17 ways to spell NAH from any N, and 17 to get to an N on a HAN. Hence for each N which leads to NAH, there are 51 ways to get the initial HAN (through 3 other N's) and 17 ways to complete NAH. Hence 17x51 ways for each N. And total 4x17x51 ways, which is 3468
References: